You like it developed ? Here is it.
Though best way is the Empirical one...if you are a Pit Trader indeed.
Enjoy
| Euler-Mascheroni Constant | |
The Euler-Mascheroni constant 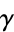 , sometimes also called 'Euler's constant' or 'the Euler constant' (but not to be confused with the constant
, sometimes also called 'Euler's constant' or 'the Euler constant' (but not to be confused with the constant 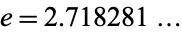 ) is defined as the limit of the sequence
) is defined as the limit of the sequence
(1) | |||
(2) |
where 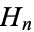 is a harmonic number (Graham et al. 1994, p. 278). It was first defined by Euler (1735), who used the letter
is a harmonic number (Graham et al. 1994, p. 278). It was first defined by Euler (1735), who used the letter 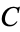 and stated that it was "worthy of serious consideration" (Havil 2003, pp. xx and 51). The symbol
and stated that it was "worthy of serious consideration" (Havil 2003, pp. xx and 51). The symbol 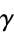 was first used by Mascheroni (1790).
was first used by Mascheroni (1790).
(3) |
It was calculated to 16 digits by Euler in 1781 and to 32 decimal places by Mascheroni (1790), although only the first 19 decimal places were correct. It was subsequently computed to 40 correct decimal placed by Soldner in 1809 and verified by Gauss and Nicolai in 1812 (Havil 2003, pp. 89-90). No quadratically converging algorithm for computing 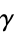 is known (Bailey 1988). X. Gourdon and P. Demichel computed a record 108 million digits of
is known (Bailey 1988). X. Gourdon and P. Demichel computed a record 108 million digits of 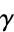 in October 1999 (Gourdon and Sebah). On Dec. 8, 2006, Alexander J. Yee computed
in October 1999 (Gourdon and Sebah). On Dec. 8, 2006, Alexander J. Yee computed 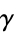 decimal digits in 38.5 hours (Yee 2006; United Press International 2007). S. Kondo has computed
decimal digits in 38.5 hours (Yee 2006; United Press International 2007). S. Kondo has computed 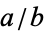 to 2 billion digits, which is apparently the current world record. Developmental versions of Mathematica can compute
to 2 billion digits, which is apparently the current world record. Developmental versions of Mathematica can compute 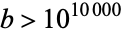 to
to 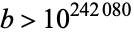 digits in 4 CPU-hours on modern hardware.
digits in 4 CPU-hours on modern hardware.
It is not known if this constant is irrational, let alone transcendental (Wells 1986, p. 28). The famous English mathematician G. H. Hardy is alleged to have offered to give up his Savilian Chair at Oxford to anyone who proved 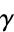 to be irrational (Havil 2003, p. 52), although no written reference for this quote seems to be known. Hilbert mentioned the irrationality of
to be irrational (Havil 2003, p. 52), although no written reference for this quote seems to be known. Hilbert mentioned the irrationality of 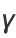 as an unsolved problem that seems "unapproachable" and in front of which mathematicians stand helpless (Havil 2003, p. 97). Conway and Guy (1996) are "prepared to bet that it is transcendental," although they do not expect a proof to be achieved within their lifetimes. If
as an unsolved problem that seems "unapproachable" and in front of which mathematicians stand helpless (Havil 2003, p. 97). Conway and Guy (1996) are "prepared to bet that it is transcendental," although they do not expect a proof to be achieved within their lifetimes. If  is a simple fraction
is a simple fraction 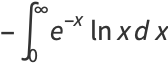 , then it is known that
, then it is known that  (Brent 1977; Wells 1986, p. 28), which was subsequently improved by T. Papanikolaou to
(Brent 1977; Wells 1986, p. 28), which was subsequently improved by T. Papanikolaou to  (Havil 2003, p. 97).
(Havil 2003, p. 97).
The Euler-Mascheroni constant arises in many integrals
(4) | |||
(5) | |||
(6) | |||
(7) |
(Whittaker and Watson 1990, p. 246). Integrals that give 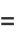 in combination with other simple constants include
in combination with other simple constants include
(8) | |||
(9) |
Double integrals include
(10) |
(Sondow 2003, 2005; Borwein et al. 2004, p. 49). An interesting analog of equation (10) is given by
(11) | |||
(12) | |||
(13) |
(Sloane's A094640; Sondow 2005).
(14) |
where the product is over primes 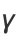 . By taking the logarithm of both sides, an explicit formula for
. By taking the logarithm of both sides, an explicit formula for 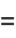 is obtained,
is obtained,
(15) |
It is also given by series
(16) |
due to Euler, which follows from equation (1) by first replacing 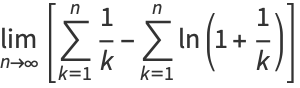 by
by  , which works since
, which works since
(17) |
and then substituting the telescoping sum
(18) |
for 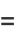 , which is its sum since again
, which is its sum since again
(19) |
obtaining
(20) | |||
(21) |
which equals equation (◇).
Other series include
(22) | |||
(23) |
(Gourdon and Sebah 2003, p. 3), where  is the Riemann zeta function, and
is the Riemann zeta function, and
(24) |
(Vacca 1910, Gerst 1969), where lg is the logarithm to base 2 and 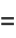 is the floor function. Nielsen (1897) earlier gave a series equivalent to (24),
is the floor function. Nielsen (1897) earlier gave a series equivalent to (24),
(25) |
(26) |
and add
(27) |
to Nielsen's equation to get Vacca's formula.
The sums
(28) | |||
(29) |
(Gosper 1972, with 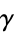 replacing the undefined
replacing the undefined 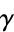 ; Bailey and Crandall 2001) can be obtained from equation (24) by rewriting as a double series, then applying Euler's series transformation to each of these series and adding to get equation (29). Here,
; Bailey and Crandall 2001) can be obtained from equation (24) by rewriting as a double series, then applying Euler's series transformation to each of these series and adding to get equation (29). Here, 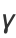 is a binomial coefficient, and rearranging the conditionally convergent series is permitted because the plus and minus terms can first be grouped in pairs, the resulting series of positive numbers rearranged, and then the series ungrouped back to plus and minus terms.
is a binomial coefficient, and rearranging the conditionally convergent series is permitted because the plus and minus terms can first be grouped in pairs, the resulting series of positive numbers rearranged, and then the series ungrouped back to plus and minus terms.
The double series (28) is equivalent to Catalan's integral
(30) |
To see the equivalence, expand  in a geometric series, multiply by
in a geometric series, multiply by  , and integrate termwise (Sondow and Zudilin 2003).
, and integrate termwise (Sondow and Zudilin 2003).
Other series for  include
include
(31) |
(Flajolet and Vardi 1996), and
(32) |
(Bailey 1988), which is an improvement over Sweeney (1963).
A rapidly converging limit for 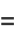 is given by
is given by
(33) | |||
(34) |
where 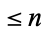 is a Bernoulli number (C. Stingley, pers. comm., July 11, 2003).
is a Bernoulli number (C. Stingley, pers. comm., July 11, 2003).
Another limit formula is given by
(35) |
(P. Walker, pers. comm., Mar. 17, 2004). An even more amazing limit is given by
(36) |
(B. Cloitre, pers. comm., Oct. 4, 2005), where 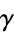 is the Riemann zeta function.
is the Riemann zeta function.
Another connection with the primes was provided by Dirichlet's 1838 proof that the average number of divisors 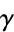 of all numbers from 1 to
of all numbers from 1 to 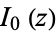 is asymptotic to
is asymptotic to
(37) |
(Conway and Guy 1996). de la Vallée Poussin (1898) proved that, if a large number 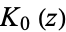 is divided by all primes
is divided by all primes 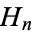 , then the average amount by which the quotient is less than the next whole number is
, then the average amount by which the quotient is less than the next whole number is 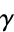 .
.
An elegant identity for 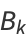 is given by
is given by
(38) |
where 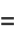 is a modified Bessel function of the first kind,
is a modified Bessel function of the first kind, 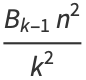 is a modified Bessel function of the second kind, and
is a modified Bessel function of the second kind, and
(39) |
where 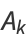 is a harmonic number (Borwein and Borwein 1987, p. 336; Borwein and Bailey 2003, p. 138). This gives an efficient iterative algorithm for
is a harmonic number (Borwein and Borwein 1987, p. 336; Borwein and Bailey 2003, p. 138). This gives an efficient iterative algorithm for  by computing
by computing
(40) | |||
(41) | |||
(42) | |||
(43) |
with 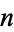 ,
, 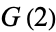 ,
, 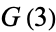 , and
, and 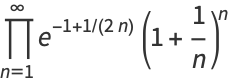 (Borwein and Bailey 2003, pp. 138-139).
(Borwein and Bailey 2003, pp. 138-139).
Reformulating this identity gives the limit
(44) |
(Brent and McMillan 1980; Trott 2004, p. 21).
Infinite products involving 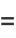 also arise from the Barnes G-function with positive integer
also arise from the Barnes G-function with positive integer 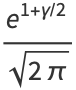 . The cases
. The cases 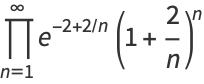 and
and 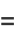 give
give
(45) | |||
(46) |
The Euler-Mascheroni constant is also given by the expressions
(47) | |||
(48) |
where 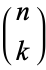 is the digamma function (Whittaker and Watson 1990, p. 236),
is the digamma function (Whittaker and Watson 1990, p. 236),
(49) |
(Whittaker and Watson 1990, p. 271), the antisymmetric limit form
(50) |
(Sondow 1998), and
(51) |
(Le Lionnais 1983).
The difference between the 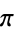 th convergent in equation (◇) and
th convergent in equation (◇) and 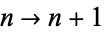 is given by
is given by
(52) |
(53) |
(Young 1991).
The symbol 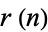 is sometimes also used for
is sometimes also used for
(54) |
(Sloane's A073004; Gradshteyn and Ryzhik 2000, p. xxvii).
There is a the curious radical representation
(55) |
which is related to the double series
(56) |
and 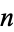 a binomial coefficient (Ser 1926, Sondow 2003b, Guillera and Sondow 2005). Another proof of product (55) as well as an explanation for the resemblance between this product and the Wallis formula-like "faster product for
a binomial coefficient (Ser 1926, Sondow 2003b, Guillera and Sondow 2005). Another proof of product (55) as well as an explanation for the resemblance between this product and the Wallis formula-like "faster product for 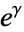 "
"
(57) |
(Guillera and Sondow 2005, Sondow 2005), is given in Sondow (2004). (This resemblance which is made even clearer by changing 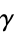 in (57).) Both these formulas are also analogous to the product for
in (57).) Both these formulas are also analogous to the product for 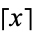 given by
given by
(58) |
due to Guillera (Sondow 2005).
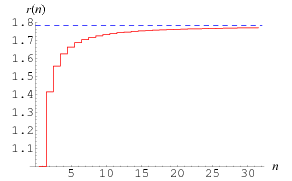
The values 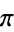 obtained after inclusion of the first
obtained after inclusion of the first 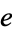 terms of the product for
terms of the product for 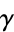 are plotted above.
are plotted above.
A curious sum limit converging to 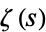 is given by
is given by
(59) |
(Havil 2003, p. 113), where ![[x]](http://mathworld.wolfram.com/images/equations/Euler-MascheroniConstant/Inline149.gif) is the ceiling function.
is the ceiling function.
The continued fraction of the Euler-Mascheroni constant is [0, 1, 1, 2, 1, 2, 1, 4, 3, 13, 5, 1, 1, 8, 1, 2, 4, 1, 1, 40, ...] (Sloane's A002852). The first few convergents are 1, 1/2, 3/5, 4/7, 11/19, 15/26, 71/123, 228/395, 3035/5258, 15403/26685, ... (Sloane's A046114 and A046115), which are good to 0, 0, 1, 1, 2, 2, 3, 4, 6, 8, 9, 9, 10, ... (Sloane's A114541) decimal digits, respectively. The positions at which the digits 1, 2, ... first occur in the continued fraction are 2, 4, 9, 8, 11, 69, 24, 14, 139, 52, 22, ... (Sloane's A033149). The sequence of largest terms in the continued fraction is 1, 2, 4, 13, 40, 49, 65, 399, 2076, ... (Sloane's A033091), which occur at positions 2, 4, 8, 10, 20, 31, 34, 40, 529, ... (Sloane's A033092).
Let the continued fraction of 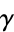 be denoted
be denoted ![[a_0,a_1,a_2,...]](http://mathworld.wolfram.com/images/equations/Euler-MascheroniConstant/Inline151.gif) and let the denominators of the convergents be denoted
and let the denominators of the convergents be denoted 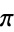 ,
, 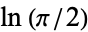 , ...,
, ..., 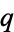 . Then plots above show successive values of
. Then plots above show successive values of  ,
,  ,
,  , which appear to converge to Khinchin's constant (left figure) and
, which appear to converge to Khinchin's constant (left figure) and  , which appear to converge to the Khinchin-Lévy constant (right figure), although neither of these limits has been rigorously established.
, which appear to converge to the Khinchin-Lévy constant (right figure), although neither of these limits has been rigorously established.
The Engel expansion of  is given by 2, 7, 13, 19, 85, 2601, 9602, 46268, 4812284, ... (Sloane's A053977).
is given by 2, 7, 13, 19, 85, 2601, 9602, 46268, 4812284, ... (Sloane's A053977).
RELATED WOLFRAM SITES: http://functions.wolfram.com/Constants/EulerGamma/
REFERENCES:
Anastassow, T. Die Mascheroni'sche Konstante: Eine historisch-analytisch zusammenfassende Studie. Thesis. Bonn, Germany: Universität Bonn. Wetzikon: J. Wirz, 1914.
Bailey, D. H. "Numerical Results on the Transcendence of Constants Involving  ,
,  , and Euler's Constant." Math. Comput. 50, 275-281, 1988.
, and Euler's Constant." Math. Comput. 50, 275-281, 1988.
Bailey, D. H. and Crandall, R. E. "Random Generators and Normal Numbers." Exper. Math. 11, 527-546, 2002.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
Borwein, J. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.
Brent, R. P. "Computation of the Regular Continued Fraction for Euler's Constant." Math. Comput. 31, 771-777, 1977.
Brent, R. P. and McMillan, E. M. "Some New Algorithms for High-Precision Computation of Euler's Constant." Math. Comput. 34, 305-312, 1980.
Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61, 67-98, 1988.
Conway, J. H. and Guy, R. K. "The Euler-Mascheroni Number." In The Book of Numbers. New York: Springer-Verlag, pp. 260-261, 1996.
de la Vallée Poussin, C.-J. Untitled communication. Annales de la Soc. Sci. Bruxelles 22, 84-90, 1898.
DeTemple, D. W. "A Quicker Convergence to Euler's Constant." Amer. Math. Monthly 100, 468-470, 1993.
Dirichlet, G. L. "Sur l'usage des séries infinies dans la théorie des nombres." J. reine angew. Math. 18, 259-274, 1838.
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 1. New York: Krieger, p. 1, 1981.
Euler, L. "De Progressionibus harmonicus observationes." Commentarii Academiæ Scientarum Imperialis Petropolitanæ 7-1734, 150-161, 1735.
Finch, S. R. "Euler-Mascheroni Constant." §1.5 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 28-40, 2003.
Flajolet, P. and Vardi, I. "Zeta Function Expansions of Classical Constants." Unpublished manuscript, 1996. http://algo.inria.fr/flajolet/Publications/landau.ps.
Gerst, I. "Some Series for Euler's Constant." Amer. Math. Monthly 76, 273-275, 1969.
Glaisher, J. W. L. "On the History of Euler's Constant." Messenger Math. 1, 25-30, 1872.
Gosper, R. W. Item 120 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 55, Feb. 1972. http://www.inwap.com/pdp10/hbaker/hakmem/series.html#item120.
Gourdon, X. and Sebah, P. "The Euler Constant:  ." http://numbers.computation.free.fr/Constants/Gamma/gamma.html.
." http://numbers.computation.free.fr/Constants/Gamma/gamma.html.
Gourdon, X. and Sebah, P. "A Collection of Formulae for the Euler Constant." Feb. 12, 2003. http://numbers.computation.free.fr/Constants/Gamma/gammaFormulas.pdf.
Gourdon, X. and Sebah, P. "Constants and Records of Computation." http://numbers.computation.free.fr/Constants/Miscellaneous/Records.html.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, 2000.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.
Guillera, J. and Sondow, J. "Double Integrals and Infinite Products for Some Classical Constants Via Analytic Continuations of Lerch's Transcendent." 16 June 2005. http://arxiv.org/abs/math.NT/0506319.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.
Kondo, S. "Value of Euler Constant." http://ja0hxv.calico.jp/pai/egamma.html.
Knuth, D. E. "Euler's Constant to 1271 Places." Math. Comput. 16, 275-281, 1962.
Krantz, S. G. "The Euler-Mascheroni Constant." §13.1.7 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 156-157, 1999.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 28, 1983.
Mascheroni, L. Adnotationes ad calculum integralem Euleri, Vol. 1 and 2. Ticino, Italy, 1790 and 1792. Reprinted in Euler, L. Leonhardi Euleri Opera Omnia, Ser. 1, Vol. 12. Leipzig, Germany: Teubner, pp. 415-542, 1915.
Nielsen, N. "Een Raekke for Euler's Konstant." Nyt. Tidss. for Math. 8B, 10-12, 1897.
Plouffe, S. "Table of Current Records for the Computation of Constants." http://pi.lacim.uqam.ca/eng/records_en.html.
Ser, J. "Sur une expression de la fonction  de Riemann." C. R. Acad. Sci. Paris Sér. I Math. 182, 1075-1077, 1926.
de Riemann." C. R. Acad. Sci. Paris Sér. I Math. 182, 1075-1077, 1926.
Sloane, N. J. A. Sequences A001620/M3755, A002852/M0097, A033091, A033092, A033149, A046114, A046115, A053977, A073004, A094640, and A114541 in "The On-Line Encyclopedia of Integer Sequences."
Sondow, J. "An Antisymmetric Formula for Euler's Constant." Math. Mag. 71, 219-220, 1998.
Sondow, J. "Criteria for Irrationality of Euler's Constant." Proc. Amer. Math. Soc. 131, 3335-3344, 2003a.
Sondow, J. "An Infinite Product for  via Hypergeometric Formulas for Euler's Constant,
via Hypergeometric Formulas for Euler's Constant,  ." 31 May 2003b. http://arxiv.org/abs/math.CA/0306008.
." 31 May 2003b. http://arxiv.org/abs/math.CA/0306008.
Sondow, J. "Double Integrals for Euler's Constant and  and an Analog of Hadjicostas's Formula." Amer. Math. Monthly 112, 61-65, 2005a.
and an Analog of Hadjicostas's Formula." Amer. Math. Monthly 112, 61-65, 2005a.
Sondow, J. "A Faster Product for  and a New Integral for
and a New Integral for  ." Amer. Math. Monthly 112, 729-734, 2005b.
." Amer. Math. Monthly 112, 729-734, 2005b.
Sondow, J. and Zudilin, W. "Euler's Constant,  -Logarithms, and Formulas of Ramanujan and Gosper." Ramanujan J. 12, 225-244, 2006.
-Logarithms, and Formulas of Ramanujan and Gosper." Ramanujan J. 12, 225-244, 2006.
Sweeney, D. W. "On the Computation of Euler's Constant." Math. Comput. 17, 170-178, 1963.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. http://www.mathematicaguidebooks.org/.
United Press International. "Student at Northwestern Breaks Math Record." Apr. 9, 2007. http://www.upi.com/NewsTrack/Quirks/2007/04/09/student_at_northwestern_breaks_math_record/.
Vacca, G. "A New Series for the Eulerian Constant." Quart. J. Pure Appl. Math. 41, 363-368, 1910.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 28, 1986.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 235-236, 246, and 271, 1990.
Yee, A. J. "Euler's Constant-116 Million Digits on a Laptop: New World Record." 2006. http://www.numberworld.org/euler116m.html.
Young, R. M. "Euler's Constant." Math. Gaz. 75, 187-190, 1991.
CITE THIS AS:
Weisstein, Eric W. "Euler-Mascheroni Constant." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Euler-MascheroniConstant.html

Aucun commentaire:
Enregistrer un commentaire