Custom Search

dimanche 20 février 2011

Hilbert Transform...

From Mathematica and Wolfram Alpha:



The Hilbert transform (and its inverse) are the integral transform
g(y)=H[f(x)]=1/piPVint_(-infty)^infty(f(x)dx)/(x-y)
(1)
f(x)=H^(-1)[g(y)]=-1/piPVint_(-infty)^infty(g(y)dy)/(y-x),
(2)
where the Cauchy principal value is taken in each of the integrals. The Hilbert transform is an improper integral.
In the following table, 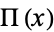Pi(x) is the rectangle function, 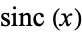sinc(x) is the sinc function, 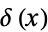delta(x) is the delta function, AdjustmentBox[I, BoxMargins -> {{0.13913, -0.13913}, {-0.5, 0.5}}]I(x) and AdjustmentBox[I, BoxMargins -> {{0.101266, -0.101266}, {0.375, -0.375}}, BoxBaselineShift -> -0.375]AdjustmentBox[I, BoxMargins -> {{0, 0}, {-0.25, 0.25}}, BoxBaselineShift -> 0.25](x) are impulse symbols, and _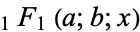1F_1(a;b;x)is a confluent hypergeometric function of the first kind.
f(x)g(y)
sinxcosy
cosx-siny
(sinx)/x(cosy-1)/y
Pi(x)1/piln|(y-1/2)/(y+1/2)|
1/(1+x^2)-y/(1+y^2)
sinc^'(x)(1-cosy-ysiny)/(y^2)
delta(x)-1/(piy)
AdjustmentBox[I, BoxMargins -> {{0.13913, -0.13913}, {-0.5, 0.5}}]I(x)y/(pi(1/4-y^2))
AdjustmentBox[I, BoxMargins -> {{0.101266, -0.101266}, {0.375, -0.375}}, BoxBaselineShift -> -0.375]AdjustmentBox[I, BoxMargins -> {{0, 0}, {-0.25, 0.25}}, BoxBaselineShift -> 0.25](x)-1/(2pi(1/4-y^2))
e^(-x^2)-e^(-y^2)erfi(y)

Posted by Waltz Lannes

Aucun commentaire:

Enregistrer un commentaire

Inscription à : Publier les commentaires (Atom)

Disqus for bookoflannes

Intense Debate Comments