Theories deal with the world on its own terms, absolutely. Models are metaphors, relative descriptions of the object of their attention that compare it to something similar already better understood via theories. Models are reductions in dimensionality that always simplify and sweep dirt under the rug. Theories tell you what something is. Models tell you merely what something is partially like.  Introduction  Writing in the New York Times ("They Tried To Outsmart Wall Street" March 9, 2009) , Denis Overbye observed:Dr. Derman, who spent 17 years at Goldman Sachs, and became managing director, was a forerunner of the many physicists and other scientists who have flooded Wall Street in recent years, moving from a world in which a discrepancy of a few percentage points in a measurement can mean a Nobel Prize or unending mockery to a world in which a few percent one way can land you in jail and a few percent the other way can win you your own private Caribbean island.Derman, Overbye noted, "fell in love with a corner of finance that dealt with stock options." "Options theory is kind of deep in some way. It was very elegant; it had the quality of physics" Derman told him. — JB EMANUEL DERMAN is physicist and a former managing director and head of the Quantitative Strategies group at Goldman, Sachs & Co., is a professor in Columbia University's Industrial Engineering and Operations Research Department, as well as a partner at Prisma Capital Partners. He is the author of My Life As A Quant. |
METAPHORS, MODELS & THEORIES Summary
1. METAPHORS
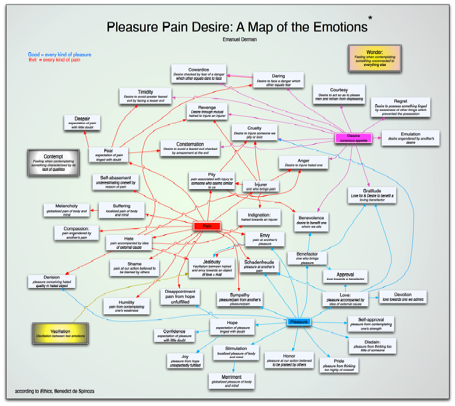
So wrote Arthur Schopenhauer, comparing life to finance in a universe that must keep its books balanced. At birth you receive a loan – consciousness and light borrowed from the void, leaving an absence in the emptiness. Nightly, by yielding temporarily to the darkness of sleep, you restore some of the emptiness and keep the absence from growing limitlessly. Finally you must pay back the principal, make the void complete again, and return the life originally lent you. By focusing on the common periodic nature of both sleep and interest payments, Schopenhauer extends the metaphor of a loan to life itself. The principal is life and consciousness, and death is the final repayment. Along the way, sleep is the periodic little death that keeps the borrower solvent. Good metaphors are expansive; they compare something we don’t understand (sleep), to something we think we do (finance). They let you see in a new light both the object of interest and the substrate you rest it on, and enlighten upwards and downwards. The common basis of Schopenhauer’s metaphoric extension is periodicity. Taking an analogy based on matching regularities and then extending it into distant regions is a time-honored trick of mathematicians. You can see it at work in the extension of the definition of the factorial function  .Using the exclamation point is traditional but clumsy. Since  is a function of  , it’s more elegant to express it via the function  defined by  , which satisfies the recursive property  . You can regard this property as almost a definition of the factorial function. If you define  , then  for all integers greater than 1 can be found from the recursive definition.The definition  works only for positive integers n. The definition  seems more malleable. Why shouldn’t there be some function  that satisfies the relation  where x is not necessarily a positive integer? Why shouldn’t the factorial function exist both for  and, say,  ?The Swiss mathematician Leonhard Euler discovered (invented?) the gamma function  that does indeed satisfy  for all  . For integer values of x, it agrees with the traditional factorial function. For non-integer or even complex values of x,  serves as a smooth extrapolation or interpolation of the factorial from integer to non-integer arguments. It’s smooth because it coincides with the factorial function for positive integer arguments, but maintains the crucial recursive property for non-integers. Mathematicians call this kind of extension called analytic continuation.The gamma function is a metaphorical extension of the factorial, in which one property, its recursion, becomes its most important feature and serves as the basis for extending it. It’s a bit like calling an automobile a horseless carriage, preserving the essence of carrying and removing the unnecessary horsefulness, or like calling a railroad ferrovia in Italian or Eisenbahn in German, focusing on the fact that it’s still a road, but one made instead of iron. Analytic continuation is a method of modeling a function. But whereas most models are restrictive – a model train is less than a real train – in mathematics, a new model can be something greater rather than diminished. That’s because mathematics deals entirely with its own world, and everything you do extends it rather than confines it. Most of the words we use to describe our feelings are metaphors or models. To say you are elated is to say you feel as though have been lifted to a high place. But why is there something good about height? Because in the gravitational field of the earth all non-floating animals recognize the physical struggle necessary to rise, and experience wonder when they see the world spread out beneath them. Being elated is feeling as if you’d overcome gravity. People dream of flying. Conversely, we speak of feeling depressed, as though we’d been pushed down to a low place. Things are looking up, we say, looking brighter, or less dark. These are metaphors too, derived from our physical senses. Metaphors nest, recursively. When we say the economy is depressed we are comparing the economy’s spirits (another metaphor) to the spirits of a person who feels as though he or she were pulled down by gravity. Language is a tower of metaphors, each “higher” one resting on older ones “below”. Not every word can be a metaphor or else language would be meaningless. At the base of the tower are words like push and down, two of the non-metaphorical word-concepts on which the tower rests. Push and down are understood by us viscerally, because we are wetware, collections of chemicals rather than silicon or computer code, that experience the world through the sensations that chemicals are capable of. You cannot have lived without knowing what it is to have struggled against gravity and responded to light and warmth, and hence to know that down and dark are bad and up and light are good. Had life arisen in outer space, free of gravity and light, there would be no perceptible down or up, and hence no possibility of depression or elation. You could be disheartened perhaps, but not depressed. You could feel full or empty, but not light or heavy, bright or dark. And you couldn’t take a dim view of your surroundings. 2. MODELS We use the word model in many contexts. A model airplane is a scaled-down version of an actual plane, similar in some respects, but not all. The four-year-old’s plastic plane, the twelve-year-old’s radio-controlled glider and the aeronautical engineer’s wind-tunnel airplane are all model airplanes, though they differ from each other. The similarities to the real thing are important, but different users require different similarities. What do we mean when we call some construct a model? The Model T is a version of a Ford, one of a class of things belonging to the Ford category. Model T is an instance, less general, not everything a Ford might be. A fashion model can be an actual person used to display clothing or cosmetics. It’s not everything a person might be. When you’re a model, only parts of you are important. A person is complete, the real thing. An artist’s model is a proxy for the real thing. A mannequin is a proxy for a proxy. (The work of art that uses the proxy becomes a real thing again.) A computer model of the weather tries to predict the weather in the future from the weather today. “Weather” is an abstraction for a collection of an indefinite number of qualities and quantities and the way they vary over the short term, among them temperature, pressure, humidity, wind speed. A weather model’s equations focus on a limited number of features of a limitlessly complex system. Even with the right equation, there is always the danger that one has omitted something ostensibly negligible but whose tail effects over long times are crucially important. An economic model aims to do for the economy what the weather model does for the weather. It too embodies a set of equations that attempts to represent the behavior of the people and institutions interacting in an economy. But just as the notion of weather is more abstract than the notion of an airplane, so the concept of an economy is even more diffuse. Money, supply, demand and utility, just a few of the many variables in an economic model, are much harder to define (let alone quantify) than temperature and pressure. A “market” and an “economy” are even more clearly a construct of the mind. When you model the economy you are modeling abstractions. Hayek pointed out that in the physical sciences the macroscopic concepts (gases, pressure, etc.) are concrete and the microscopic one (atoms and molecules) abstractions. But in economics, he argues, individuals are concrete and the “economy” is the abstraction. The Black-Scholes Model tells you how to estimate the value of an option in terms of its underlying risk. It’s a recipe, an engineering model, a Sol LeWitt painting that contains instructions for how to create a work of art. Just as a weather model makes assumptions about how fluids flow and how heat undergoes convection, just as a souffle recipe makes assumptions about what happens when you whip egg whites, so the Black-Scholes model makes assumptions about how stock prices fluctuate up and/or down. But our assumptions about the behavior of stock markets are much less believable than our assumptions about how egg whites turn fluffy. Fluids and egg protein don’t care what people think about them; markets and stock prices do. Like a weather model (but even more so), Black-Scholes is a limited, ingeniously clever mental model of a complex system, a small box that tries to imitate the actual world outside. The Standard Model, for which Sheldon Glashow, Abdus Salam and Steven Weinberg received the 1979 Nobel prize in physics, is a unified description of the smallest elementary particles (quarks and leptons) and the forces between them. The description incorporates into one coherent framework Maxwell’s 19th century theory of electromagnetism, the 1928 Dirac theory of the electron and Fermi’s 1934 theory of beta decay in which all of these apparently disparate forces are only superficially different aspects of a single more general force. The standard model is not really a “model” at all, but rather a description, and hence a theory. A theory, as I will argue below, attempts to provide an accurate description of the nature of things, unifying the outward with the inward, not just saving the appearances but identifying their essence. A model arises out of conscious analogy. A theory arises out of a deep intuitive identification of the inner and the outer. 3. WHY IS A MODEL A MODEL? A model airplane, however complex, is simple when compared to the real thing. There is a gap between the model and the object of its focus. The model is not the object, though we may wish it were. A model is a metaphor of limited applicability, not the thing itself. Calling a computer an electronic brain once cast light on the function of computers. Nevertheless, a computer is not an electronic brain. Calling the brain a computer is a model too. In tackling the mysterious world via models we do our best to explain the thus-far incomprehensible by describing it in terms of the things we already partially comprehend. Models, like metaphors, take the properties of something rich and project them onto something strange. A model focuses on parts rather than the whole. It is a caricature which overemphasizes some features at the expense of others. A model is a fetish in which the importance of one key part of the object of interest is obsessively exaggerated until it comes to represent the object’s quintessence, a shoe or corset standing in for a woman. (Is that perhaps why most modelers are male?). But the shoe or corset isn’t the woman, just the most important part of the woman for this model user. The most valuable knowledge is unconscious. Until you can do something without thinking, you can’t move farther up the hierarchy of metaphors of description in language or science. In Zen in the Art of Archery, Eugen Herrigel recounts the struggle to make mental knowledge visceral. Thinking for yourself is hard work. Models provide ways of letting other people do the thinking for you. With Feynman diagrams, almost anyone can calculate elementary particle cross sections mechanically. In physics or finance, the first major struggle is to gain some intuition about how to proceed; the second struggle is to transform that intuition into something more formulaic, a set of rules anyone can follow, rules that no longer require the original insight itself. One person’s breakthrough becomes everybody’s possession. The world is multi-dimensional. Models allow us to project the object into a smaller space and then extrapolate or interpolate within it. At some point the extrapolation will break down. What’s amazing is how well it sometimes works, especially in the physical sciences. But extrapolation based on limited information is dangerous; extrapolation depends on a model, not a fact. Estrogen supplements cause their own problems, and margarine only seemed better than butter. When unconsciously used models result in paradoxes or conflicts, it becomes necessary to expose and then examine unconscious assumptions. This is what Einstein did with the concept of simultaneity, what Lee and Yang did with parity invariance. 4. WHY IS A THEORY A THEORY? Models are analogies, and always describe something relative to something else. Theories, in contrast, are the real thing. They don’t compare; they describe the essence, without reference. Every fact, as Goethe wrote, is a theory. In that sense, a theory is the ultimate non-metaphor. Moses, tending the flock of his father-in-law Jethro near the mountain of Horeb, saw a burning bush whose flame would not consume it. God, from within the bush, declared himself to Moses and commanded him to deliver the Israelites from Pharaoh. Whom shall I tell them sent me? asks Moses. Tell them: I am that which I am, said the voice. God is riffing on his true name: the Hebrew word for I will be is EHYH. Its root is HVH, the last three letters of God’s name. HVH means being, and is also the name of thepresent tense in Hebrew grammar. YHVH (Yahweh or Jehovah) is the irreducible substance, the ultimate non-metaphor too, the bottom-level primitive out of which everything else is constructed. Hence, no graven images, no models, are possible. You can’t ask ‘Why?’ about YHVH; you can ask only ‘How?’. Theories tell you what something is. Models tell you only what something is more or less like. Unless you constantly remember that, therein lies their danger. My favorite theory is Dirac’s 1928 theory of the electron, still correct today. He sought an equation that satisfied both quantum mechanics and special relativity. The one he found had four solutions. Two of them described the electron that physicists already knew about, a particle with negative charge and two spin states. But Dirac’s equation had two additional solutions, similar to the ones he’d already found, but with incomprehensibly negative energy. The positive-energy solutions described the electron so well that Dirac felt obliged to make sense of the negative-energy ones too. Dirac postulated that the void, the medium that we call empty space, what physicists call the vacuum, is in fact filled to its rim with negative-energy electrons, and they constitute an infinite sea. This metaphorical Dirac sea is the vacuum we inhabit, and, accustomed to it, we don’t notice the infinite number of negative charges surrounding us. (We smell only pollutants, not air itself.) If this is true, argued Dirac, then when you shoot light into the vacuum and eject a negative energy electron, a hole is left behind. This absence of an electron and its negative charge behaves exactly like an electron with positive charge. Anderson discovered this so-called positron in 1932, and astounded all the physicists uncomfortable with what had been a metaphorical stretch. Just as life is a temporary hole in the darkness, so here too absence becomes a presence. Dirac’s equation transcended its metaphor and became a theory of reality. A brain may be like a computer, an atom may be like a miniature solar system, but an electron is the Dirac equation. Dirac’s theory of the electron stands on its own two feet, beyond metaphor, the thing itself. Like God in the burning bush identifying himself to Moses, the theory of the electron pronounces, “I am that which I am.” Theories are deep and inexplicable, difficult to find; they require verification; they are right when they are right. Models are shallow and somewhat easier to invent; they require explanation. We need models as well as theories. 5. SPINOZA'S THEORY OF THE AFFECTS Spinoza approached what he called the affects, human emotions, in the same way that Euclid approached triangles and squares, aiming to understand their inter-relations by means of principles, logic and deduction. Spinoza’s avowed aim was to find a method to escape the violent sway emotions inflict on human beings caught in their grip. The Primitives Spinoza’s primitives are pain, pleasure and desire. Every adult with a human body knows by direct experience what these feelings are, though Spinoza, following Euclid’s definitions of points and lines, makes an attempt to define them. Desire, he writes, is appetite conscious of itself. Its cohorts are two more primitives: pleasure and pain. Though he defines them, as is the case with Euclid’s points and lines, we can recognize neither pain nor pleasure from their verbal definitions; we need to have experienced them directly and had them named. They lie beneath all the other affects and can conveniently be thought of as closer to organic conditions than psychic ones. Spinoza distinguishes finely between local and global sensations. “Pleasure andpain,” he writes, “Are ascribed to a man when one part of him is affected more than the rest, whereas cheerfulness and melancholy are ascribed to him when all are equally affected.” Suffering, therefore, is localized pain, while melancholy is globalizedpain. His definitions of good and bad are utilitarian at the individual level. “By good I here mean every kind of pleasure, and all that conduces thereto, especially that which satisfies our longings, whatsoever they may be. By evil, I mean every kind of pain, especially that which frustrates our longings.” Good is that which brings pleasure andbad is that which brings pain. The Derivatives The primitives are the most fundamental affects, and the more complex emotions bear a more indirect link to the three just named. Just as financial stock options are derivatives that depend on the underlying stock price, so more complex human emotions derive their force from their relation to the three underlying sensations of pain, pleasure and desire. Spinoza elaborates: Love is pleasure associated with an external object. Hate is pain associated with an external object. Hope is the expectation of future pleasure when the outcome is uncertain and doubtful. Joy is the pleasure we experience when that doubtful expectation is fulfilled. Disappointment is the pain of unfulfilled pleasure. Pity is pain accompanied by the idea of evil which has befallen someone else whom we conceive to be like ourselves. More complex emotions, like exotic financial derivatives, depend on two underlying primitives. Envy is pain at another's pleasure, like a convertible bond whose value depends on stock prices and interest rates. Conversely, though Spinoza doesn’t name it, Schadenfreude is pleasure at another’spain. Cruelty involves all three primitives: Spinoza defines it as the desire to inflict pain on someone we love or pity. Financially speaking, Cruelty is a convertible bond whose value depends on the stock price of the underlying stock, riskless interest rates and credit spreads. Spinoza adds to his system three additional primitives that are meta-emotions. The first is Vacillation, the state of oscillation between two emotions. Thus Jealousy, he explains, is the vacillation between hate and envy towards an object of love in the presence of a rival for it. Jealousy is a derivative of envy, and envy is a derivative ofpleasure and pain. If we follow the links far enough, we end up always at pain,pleasure and desire. The second addition is Wonder. Wonder is what we experience when confronted by something that fills the mind to the exclusion of all else, something unrelated to anything else. Wonder is what we experience in the presence of Yahweh in the burning bush, who is what he is, and bears no relation to anything else. Spinoza’s final primitive is Contempt, the feeling we have when we contemplate something that most forcibly reminds us of all the qualities it lacks. An absence becomes a nameable presence. I call what Spinoza created a theory rather than a model. He doesn’t make analogies; he doesn’t attempt to explain how humans behave by comparing them to some other system we already understand. He begins with observations about human beings, obtained through experience, introspection and intuition. He produced a theory accessible to everyone because it analyzes everyday human experiences. The figure below illustrates the dependency of all the emotions on Desire, Pleasureand Pain.
6. Intuition It takes intuition to discover theories. Intuition may sound casual but it results from intimate knowledge acquired by careful observation and painstaking effort. John Maynard Keynes wrote a speech for the Newton tercentary in which he commented on Newton’s qualities:
This perception – that his insight arose independent of his proof – was also James Clerk Maxwell’s opinion about André-Marie Ampère, who, in 1820, discovered the connection between electricity and magnetism. Referring to Ampère as the “Newton of electricity”, Maxwell, who extended Ampère’s discoveries into Maxwell’s equations and found that they described light, wrote: “We can scarcely believe that Ampere really discovered the law of action by means of the experiments which he describes. We are led to suspect, what, indeed, he tells us himself, that he discovered the law by some process which he has not shown us, and that when he had afterwards built up a perfect demonstration, he removed all traces of the scaffolding by which he had built it.” When you struggle with a field of inquiry for a long long time and you eventually master and incorporate not only its formalism but its content, you can make use of it to build things one level higher. Intuition is a merging of the understander with the understood. It is the deepest kind of knowledge. 7. Models in Finance There are no genuine theories in finance. Financial models are always models of comparison, of relative value. They are metaphors. The efficient market model assumes stock prices behave like smoke diffusing through a room. These are comparisons that have some reasonableness, but they’re not even remotely fact. Newton’s laws and Maxwell’s equations are. There is almost no gap between the object and their description. You can say that stock prices behave like smoke. You cannot say that light behaves like Maxwell’s equations. Light is Maxwell’s equations. All concepts, perhaps all things, are mental. But there are no genuine theories in finance because finance is concerned with value, an even more subjective concept than heat or pressure. Furthermore, it is very difficult to find the scientific laws or even regularities governing the behavior of economies: there are very few isolated economic machines, and so one cannot carry out the repeated experiments that science requires. History is important in economics. Credit markets tomorrow won't behave like credit markets last year because we have learned what happened last year, and cannot get back to the initial conditions of a year ago. Human beings and societies learn; physical systems by and large don't. For an experiment to be approximately repeatable, history has to be unimportant. That requires that the system couple very weakly to the rest of the universe. A coin flip can be repeated ad infinitum under almost the same conditions, because external conditions affect its outcome hardly at all. That’s not the case in finance. What is the point of a model in finance? It takes only a little experience to see that it’s not the same as the point of a model in physics or chemistry. Mostly, the point of a model is not prediction or divination. Here’s a simple but prototypical financial model that has most of the characteristics of more sophisticated models. How do you estimate the price of a seven-room apartment on Park Ave. if someone tells you the market price of a typical two-room apartment in Battery Park City? Most likely, you figure out the price per square foot of the two-room apartment. Then you multiply by the square footage of the Park Ave. apartment. Finally you make some rule-of-thumb higher-order corrections for location, park views, light, facilities and so on. You might develop a model for those too. The model’s critical parameter is the implied price per square foot. You calibrate the model to Battery Park City. Then you use it to interpolate or extrapolate to Park Ave. The price per square foot is implied from the market price of the Battery Park City apartments; it’s not the realized construction price per square foot because there are other variables – exposure, quality of construction, neighborhood – that are subsumed into that one implied number. Calibration is dangerous; it’s always the fitting a wrong model to the only world we know, and then using it to extrapolate or interpolate. The closer your model to the behavior of the world, the less dangerous your extrapolation. The Aim of Financial Models The way property markets use implied price per square foot illustrates the functions of financial models more generally. Models are used to rank securities by value. Apartments have manifold features. Implied price per square foot can be used to rank and compare many similar but not identical apartments. It provides a simple one-dimensional scale on which to begin ranking apartments by value. The single number given by implied price per square foot doesn’t truly reflect the value of the apartment; it provides a starting point after which more qualitative factors must be taken into account. Models are used to interpolate from liquid prices to illiquid ones In finance, models are used less for divination than in order to interpolate or extrapolate from the known prices of liquid securities to the values of illiquid securities at the current time – in the example above from the Battery Park City price to the Park Ave. value. The Black-Scholes model proceeds from a known stock price and a riskless bond price to the unknown price of a hybrid, an option, similar to the way one estimates the value of fruit salad from its constituent fruits. No model is correct – a model is not a theory – but models can provide immensely helpful ways of initial estimates of value. Models transform intuitive linear quantities into nonlinear dollar values In finance a model is also a means of translating acquired intuition into dollar values. The apartment-value model transforms price per square foot into the value of the apartment. It’s easier to begin with an estimate of price per square foot because that quantity captures so much of the variability of apartment prices. Similarly, it’s easier to convert one’s intuition about future volatility into current options prices than it is to guess at the appropriate prices themselves. 8. THE ONE LAW OF FINANCE Research papers in quantitative finance look superficially like those in natural science, but the similarity is deceptive. There are no deep laws or theories in finance that can be expressed in mathematics. The one law you can rely on in finance is the law of one price, which roughly put, dictates: “If you want to know the value of a financial security, use the known price of another security that’s as similar to it as possible.” The wonderful thing about this law – it’s valuation by analogy – when compared with almost everything else in economics, is that it dispenses with utility functions, the unobservable hidden variable whose ghostly presence permeates most of faux-quantitative economic theory. The law of one price is not a law of nature. It’s a general reflection on the practices of human beings, who, when they have enough time and enough information, will grab a bargain when they see one. The law usually holds in the long run, in well-oiled markets with enough savvy participants, but there are always short- or even longer-term exceptions that persist. How do you use the law of one price to determine value? If you want to estimate the unknown value of a target security, you must find some other replicating portfolio, a collection of more liquid securities that, collectively, is similar to, i.e. has the same future payoffs as the target, no matter how the future turns out. The target’s value is then simply that value of the replicating portfolio. Where do models enter? It takes a model to demonstrate similarity, to show that the target and the replicating portfolio have identical future payoffs under all circumstances. To demonstrate the identity of future payoffs, you must (1) specify what you mean by “all circumstances,” for each security, and (2) you must find a strategy for creating a replicating portfolio that, in each future scenario or eventuality, will have payoffs identical to those of the target. That’s what the Black-Scholes options model does – it tells you precisely how to replicate an option out of stocks and bonds, under certain assumptions. It’s like a recipe that tells you how to make fruit salad – an option – out of fruit, the stocks and bonds. And, ingeniously used, it tells you how to do the inverse – to figure out the value of one type of fruit given the price of other fruits and fruit salad. Most of the mathematical complexity in finance involves the description of the range of future behavior of each security’s price. Trying to specify all circumstances always reminds me of the 1967 movie Bedazzled, starring Peter Cook and Dudley Moore. In this retelling of the German legend of Faust, Dudley Moore plays a short-order cook at a Wimpy’s chain restaurant in London who sells his soul to the devil in exchange for seven chances to specify the circumstances under which he can achieve his romantic aims with the Wimpy’s waitress he desires. Each time that the devil asks him to specify the romantic scenarios under which he believes he will succeed, he cannot get them quite specific enough. He says he wants to be alone with the waitress in a beautiful place where they are both in love with each other. He gets what he wants—with a snap of the devil’s fingers, he and his beloved are instantly transported to a country estate where he is a guest of the owner, her husband, whom her principles will not allow her to betray. In the final episode, he wishes for them to be alone together and in love with each other in a quiet place where no one will bother them. He gets his wish: The devil makes them both nuns in a convent where everyone has taken a vow of silence. This difficulty is the same difficulty we have when specifying future scenarios in financial models—like the devil, markets always eventually outwit us. Even if markets are not strictly random, their vagaries are too rich to capture in a few sentences or equations. So die the dreams of financial theories. Only imperfect models remain. 9. THE RIGHT WAY TO USE MODELS Given that finance’s best tools are shaky models, the best strategy is to use models as little as possible, and to replicate making as little assumptions as you can. Here are some other rules I’ve found to be useful as a practitioner. Avoid too much axiomatization Axiomatization is for mathematics. Finance is about the real world. Every financial axiom is pretty much wrong; the practical question is: how wrong, and can you still make use of it? Good Models are Vulgar in a Sophisticated Way In physics it pays to drop down deep, several levels below what you can observe (think of Newton, Maxwell, Dirac), formulate an elegant principle, and then rise back to the surface to work out the observable consequences. In financial valuation, which lacks deep scientific principles, it’s better to stay shallow and use models that have as direct as possible a path between observation of similarity and its consequences. Markets are by definition vulgar, and correspondingly the most useful models are wisely vulgar too, using variables that the crowd uses, like price per square foot, to describe the phenomena they observe. Build vulgar models in a sophisticated way. Of course, over time crowds and markets get smarter and the definition of vulgarity changes to encompass increasingly sophisticated concepts. Sweep Dirt Under The Rug, But Let Users Know About It One should be very humble in applying mathematics to markets, and be extremely wary of ambitious theories, which are, when you face facts, trying to model human behavior. Whenever we make a model of something involving human beings, we are trying to force the ugly stepsister's foot into Cinderella's pretty glass slipper. It doesn't fit without cutting off some essential parts. Models inevitably mask as well as expose risk. You must start with models and then overlay them with common sense and experience. The world of markets doesn’t exactly match the ideal circumstances a model assumes, but a robust model allows a savvy user to qualitatively adjust for those mismatches. A user should should know what has been assumed when he uses the model, and he should know exactly what has been swept out of view. Think of Models as Gedanken Experiments It’s impossible to make a correct financial model. Therefore, I like to think of financial models as gedanken experiments, like those Einstein carried out when he pictured himself surfing a light wave or Schrodinger when he pictured a macroscopic cat subject to quantum effects. I believe that’s the right way to use mathematical models in finance, and the way experienced practitioners do use them. Models are only models, not the thing in itself. So, we can’t expect them to be truly right. Models are better regarded as a collection of parallel thought universes you can explore. Each universe should be consistent, but the actual financial and human world, unlike the world of matter, is going to be infinitely more complex than any model you make of it. You are always trying to shoe-horn the real world into one of the models to see how useful an approximation that is. Beware of Idolatry The greatest conceptual danger is idolatry, imagining that someone can write down a theory that encapsulates human behavior and relieves you of the difficulty of constant thinking. A model may be entrancing but no matter how hard you try, you will not be able to breath true life into it. To confuse the model with a theory is to embrace a future disaster driven by the belief that humans obey mathematical rules. Financial modelers must therefore compromise, must firmly decide what small part of the financial world is of greatest current interest, decide on its key features, and make a mock-up of only those. A model cannot include everything. If you are interested in everything you are interested in too much. A successful financial model must have limited scope; you must work with simple analogies; in the end, you are trying to rank complex objects by projecting them onto a low-dimensional scale. In physics there may one day be a Theory of Everything; in finance and the social sciences, you have to work hard to have a usable Model of Anything. |
| COURTESY OF THIRD CULTURE, ALL RIGHTS RESERVED TO THIRD CULTURE AND MR. BERMAN and whoesle is entitled to . WE DO NOT OWN THIS INTELLECTUAL CONTRIBUTION , POST IT HERE WITH NO COMMERCIAL OR PROFIT INTENTS. |
Aucun commentaire:
Enregistrer un commentaire