In Search of Power-laws: WikiLeaks Edition
Yesterday, a commenter reminded me of the very popular hobby among scientists of searching for power-law distributions in large event data. While the commonality of scale invariance in event data is quite well known—particularly with respect to conflict data—this has not prevented many researchers from seeking and finding these patterns in data.
As the commenter notes, it is likely that the WikiLeaks data will soon be annexed into this line of research. Before other researchers examine the distributional properties of these data more thoroughly, it is worth doing a quick exploration to show some of the issues in power-law fishing, and how to avoid them. First, we begin by plotting the WikiLeaks casualty data using the traditional log-log transformation and fitting a linear regressio.
| KIA Only | All Casualties |
 |  |
The search for power-law distributions often focuses on the scaling parameter: 
. Scaling parameters where 2 < 
< 3 are generally accepted as fitting a power-law, thus the search is for values in that range.
. Scaling parameters where 2 < < 3 are generally accepted as fitting a power-law, thus the search is for values in that range.When using linear regression to fit the distribution this parameter is calculated simply as the slope of the linear fit to the logged data. The above panels show this analysis for two different version of the data. On the left, the data are restricted to only observations with, in the words of Lewis Richardson, “deadly quarrels.” That is, WikiLeaks events where a death occurred, which accounts for friendly, enemy, host nation and civilian deathsg. Interestingly, we find that for the KIA data the scaling parameter falls just outside the necessary range to be classified as a power-law.
At this point we might conclude that the data does not fit our assumptions and move on to test other distributions. If we were particularly motivated to find a power-law in this data, however, one option would be to go back and loosen our restriction on the data to include not just KIA’s but all casualties, i.e., non-deadly quarrels. The assumption being that with more data points the “tail” of the distribution would be longer and thus more likely to fit a power-law. The right panel above illustrates this analysis, and as you can see in this case we find that the data do fit a power-law, with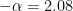 
.
.Unfortunately, even if suspending disbelief enough to accept the altogether dubious inclusion of more data points to force-fit a power-law, everything we have done up to this point is wrong. As was brilliantly detailed by Clauset, et al in “Power-law distributions in empirical data,” linear fits to log transformed data are extremely error-prone. As such, rather than rely on the above findings we will use the method detailed by these authors for properly fitting power-law on the WikiLeaks data.
In this case we need to do three things: 1) find the appropriate lower-bound for the value of 
for our data, which in this case are events with casualties; 2) fit the scaling parameter with 
; 3) perform a goodness-of-fit test to test whether our empirical observations actually fit the parameterization of the distribution.
for our data, which in this case are events with casualties; 2) fit the scaling parameter with ; 3) perform a goodness-of-fit test to test whether our empirical observations actually fit the parameterization of the distribution.For the first step we are fortunate, as we know the appropriate minimum value 
, since these are discrete event data and we are counting the number of observed casualties in the data. Equally convenient, this allows for a straightforward maximum-likelihood estimation of the scaling parameter via a variant of the well-known Hill estimator. This functionality is built-into R’s igraph package so we can compute the new scaling parameters easily.
, since these are discrete event data and we are counting the number of observed casualties in the data. Equally convenient, this allows for a straightforward maximum-likelihood estimation of the scaling parameter via a variant of the well-known Hill estimator. This functionality is built-into R’s igraph package so we can compute the new scaling parameters easily.| KIA Only | All Casualties | |
| MLE | 1.823 | 1.78 |
Using this more accurate methods for estimating the scaling parameter reveals that—in fact—neither set of data on the frequency and magnitude of violent events in Afghanistan fit a power-law. As a result, goodness-of-fit tests for power-law with this data are unnecessary, but as described in Clauset, et al. using a Kolmogorov–Smirnov test to measure the distance between theorized and observed distributions is a useful tool for checking fits to other distributions. There are several alternative distributions that may better fit these data, many of which are specified for simulation in the degreenet R package, but I leave that as an exercise to the reader.
There are two primary things to take away from this exercise: 1) power-laws are much less frequently observed than is commonly thought, and careful estimation of scaling parameters and goodness-of-fit should be performed to check; 2) it appears that the WikiLeaks data fall well short of proving, or even reinforcing, previous conclusions about the underlying dynamics of violent conflict.
As always, the code used to generate this analysis is available on Github.
Automatically Generated Related posts:
Aucun commentaire:
Enregistrer un commentaire